简述

本文记录我记录我学习 坐标体系和矩阵转换的过程,加深学习便于后续查询,可能有些描述不够准确,或者内容不够充实,还请多多指正,共同学习

矩阵变换

我们将物体坐标进行一系列变换,达到自己期望的位置,需要使用到矩阵.先说一下矩阵的公式.这里我是本着了解的心态去学习的,因为已经有趁手的数学工具了,把重要的学完~ 我会再来研究这里的.

矩阵相乘

这是一个简单的矩阵相乘例子,

这是矩阵乘法过程~

注意:

1, 矩阵相乘不遵守交换律 即 A B ≠ B A
2, 只有当左侧矩阵列数 等于 右侧矩阵行数 两矩阵才能相乘.

在我们对坐标进行缩放,位移,旋转 等变换时,我们多用4x4矩阵来进行~

缩放

我们把缩放变量表示为(S1,S2,S3)我们可以为任意向量(x,y,z)定义一个缩放矩阵：

位移

如果我们把位移向量表示为(Tx,Ty,Tz)，我们就能把位移矩阵定义为：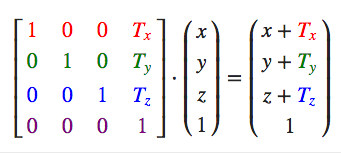

旋转

绕X轴旋转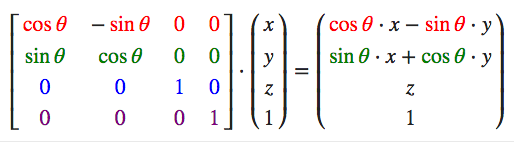

绕y轴旋转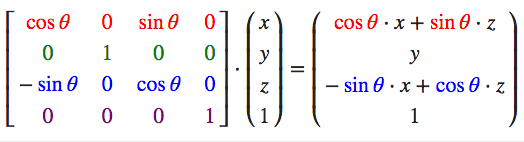

绕z轴旋转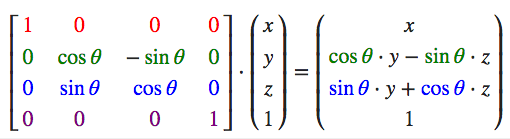

将旋转分为绕3个轴进行旋转,以达到自己希望的位置,见下面这个公式，(Rx,Ry,Rz)代表任意旋转轴：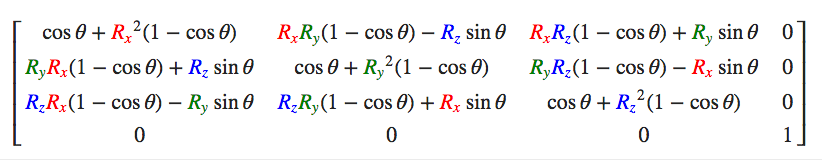

这种处理方式,简单容易理解,但是 会出现一个问题万向节死锁.

举个栗子~ 加入在三维空间中有一个平行于X中的向量,然后将它绕Y轴旋转至它平行于Z轴,这时绕z轴的任何旋转都不会改变 向量的方向了. 在正常情况下,关于3个轴的旋转过程应该是可以任意组合的,最终旋转结果都是一致的,但是当出现了万向节死锁后, 就会导致各个轴旋转顺序 组合不同,而最终旋转结果不同~ 大家可以找根笔试一试~也可以看看这里:欧拉角与万向节死锁（图文版

那么如何解决呢~ 使用四元数 旋转矩阵与四元数 因为复变函数早已还给老师~ 后续再研究补充~~

齐次坐标

在上面关于描述3D坐标的向量 是四维向量,多出一个分量w,w分量的用处是来创造3D视觉效果的,根据w分量的大小对物体进行拉伸,最后将w=1的截面进行展示,从而产生物体远近效果. 这篇文章我觉得介绍的比较详细 写给大家看的“透视除法” —— 齐次坐标和投影

组合

我将不同变换的矩阵组合起来~ 将一个放大2倍的矩阵 和位移(1,2,3)的矩阵组合起来~,得到新的变换矩阵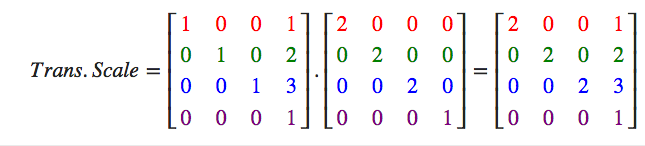

将得到的变换矩阵 进行验证

因为矩阵相乘是不遵守交换律的,所以在矩阵组合时,顺序就十分重要, 建议 先缩放 –> 再旋转 –> 再位移. 并且矩阵的顺序是从右到左的 所以应该是
位移矩阵 旋转矩阵 缩放矩阵 = 所需矩阵

补充

为什么我们要用矩阵来进行着一系列的变换呢? 据我了解 是因为这样做,将 旋转,位移,缩放加以统一.简化计算流程,提高计算机的计算效率.

最后总结:像这样利用矩阵进行位移,缩放,旋转 这一系列的变换叫做:仿射变换

坐标体系

OpenGL 顶点着色器 希望接受的的顶点 都是标准化设备坐标(Normalized Device Coordinate, NDC)的坐标,也就是(x,y,z)都是在 -1~1之间变换.在此之外的顶点丢弃,并且按照传入的顶点进行绘制.

将3D的物体坐标转换到理想的绘制效果需要进行一些列的转换过程.
局部空间(Local Space)/物体空间(Object Space) —> 世界空间(World Space) —> 观察空间(View Space)/视觉空间(Eye Space) —>裁剪空间(Clip Space) —> 屏幕空间(Screen Space)

OpenGL是不提供数学工具的~ 我们可以使用 GLM(OpenGL Mathematics) GLM官网 我用的是0.9.9版本~

示意图: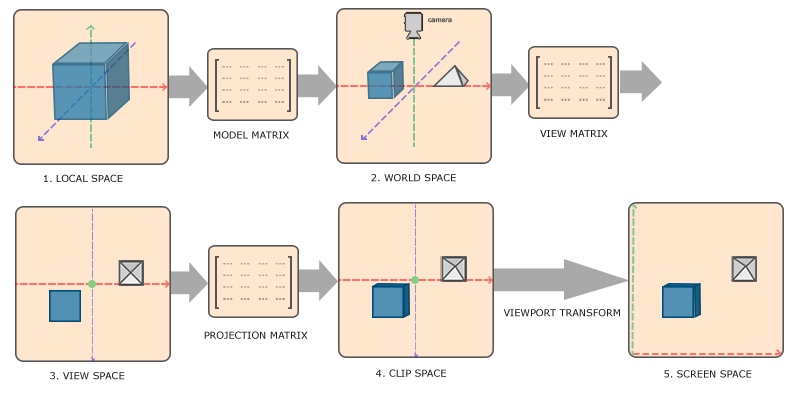

局部空间

局部空间: 就表示物体在自己本身坐标系里的坐标,比较像view的bounds属性.可以理解为建模时模型的坐标.

世界空间

世界空间: 表示物体需要展示世界里的坐标,比较像view的frame属性,好比我们的模型是个房子,将它放到小镇(世界)中, 这时它的坐标就是在世界空间的坐标.

将局部空间坐标转换为世界空间坐标需要进行一系列转换,就像在象棋棋盘上放棋子,我们需要将棋子旋转,位移…操作才能将棋子放到正确的位置上.

观察空间

在最终展示时,我们展示的是用户观察的界面, 我们需要将世界空间的坐标 转换为 以用户坐标观察视野产生的结果.

裁剪空间

在OpenGL 中所期望的坐标是 标准化设备坐标, 所以我们 需要将自己的坐标集进行转换,将需要显示的坐标 落在 -1.0~1.0之间.

如果只是图元(Primitive)，例如三角形，的一部分超出了裁剪体积(Clipping Volume)，则OpenGL会重新构建这个三角形为一个或多个三角形让其能够适合这个裁剪范围,就像三角形的角被切了一刀变成四边形那样~

投影

在裁剪时,我们是将3D空间的物体 转换为 2D空间的平面图像, 这样的过程叫做投影, 像投影截取的显示的3D空间 平截头体,它就像一个容器,在这里面的所有坐标都不会被裁剪掉~

正射投影

在裁剪空间阶段,获得平截头体的方式, 就是通过 正射投影. 使用正射投影矩阵创天平截头体 需要指定 近平面宽高, 远平面宽高.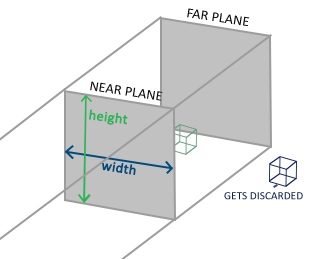

通过正射投影矩阵,将3D空间的坐标 映射到2D平面中,但是这样产生的问题是 并没有远近缩放的效果,这时就需要 透视投影.

透视投影

透视投影,就是利用齐次坐标w 来生成远近效果的, 离观察者越远的顶点 w分量越大.在显示时,顶点坐标的每个分量都会除以w分量,进而使 远端的物体小,近端的物体大.

透视矩阵 会根据平截头体的顶点的远近,对顶点w分量进行修改

组合

若上面每一个步骤都产生一个变换矩阵的话,那么最终的顶点坐标应该是这个样子的
目标顶点 = 投影矩阵 观察矩阵 模型矩阵 *原始顶点

标准化设备坐标

1
2

//此方法创建的窗口就是对应的OpenGL 的标准化设备窗口
glViewport(0, 0, self.frame.size.width, self.frame.size.height);

模型矩阵

模型矩阵 包含了 位移,缩放,旋转操作, 它将应用到物体的所有定点上. 该矩阵的目的就是将原来位于 世界空间(0,0,0)点的物体 移动到它应该出现的位置.

观察矩阵

观察矩阵就像是 3D世界里的摄像机,最终显示的画面 就是摄影机的位置 和 方向 观察的画面~ 观察矩阵的创建就需要 GLM 提供的LooK AT 函数:

tmat4x4 lookAt(tvec3 const & eye, tvec3 const & center, tvec3 const & up)

该函数需要输入 3个 vec3变量,返回观察矩阵:

参数1: 相机在世界坐标系的位置
参数2: 相机镜头指向的位置
参数3: 世界的上向量,上向量的方向 在显示时 是指向屏幕上方的向量

通过对这三个变量控制,就可以实现我们希望的效果,我在练习时 实现的是类似 游戏CS里 摄像头移动的方式

投影矩阵

glm::mat4 proj = glm::perspective(glm::radians(45.0f), (float)width/(float)height, 0.1f, 100.0f);

此函数其实是创建了一个 定义了 可视控件的 平头截体,此空间以外的东西都将被抛弃~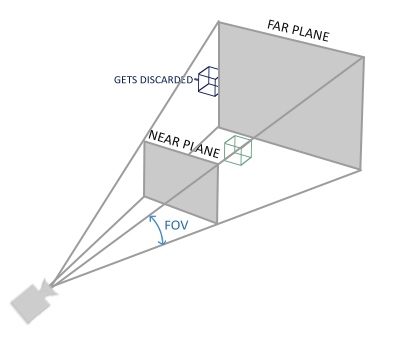

参数:

第一个参数定义了fov值,它表示了视野(Field of View),就相当于摄影机的摄影角度~~
第二个参数 为宽高比, 由视口的宽/高所得
第三和第四个参数 设置了平截头体的近和远平面。我们通常设置近距离为0.1f，而远距离设为100.0f。所有在近平面和远平面内且处于平截头体内的顶点都会被渲染.

最后经过透视矩阵的处理,就产生了 物体 远小近大的效果了~

代码

这里就捡与本文相关的说~

顶点着色器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

#version 300 es

layout(location = 0) in vec3 position;
layout(location = 1) in vec3 color;
layout(location = 2) in vec2 texCoord;  //纹理坐标

//uniform mat4 transform;

uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;

out vec3 outColor;
out vec2 outTexCoord;

void main()
{
    gl_Position = projection*view*model*vec4(position,1.0);
    outColor = color;
    outTexCoord = texCoord;
}

开启深度测试

OpenGL存储它的所有深度信息于一个Z缓冲(Z-buffer)中，也被称为深度缓冲(Depth Buffer)。GLFW会自动为你生成这样一个缓冲（就像它也有一个颜色缓冲来存储输出图像的颜色）。深度值存储在每个片段里面（作为片段的z值），当片段想要输出它的颜色时，OpenGL会将它的深度值和z缓冲进行比较，如果当前的片段在其它片段之后，它将会被丢弃，否则将会覆盖。这个过程称为深度测试(Depth Testing)，它是由OpenGL自动完成的。

深度测试还有其他关于 自定以的函数,以后再说~~

1
2
3
4
5
6
7
8
9
10
11

int wi,he;
//检索有关绑定缓冲区的对象的信息 ,这里获得了layer的宽高
glGetRenderbufferParameteriv(GL_RENDERBUFFER, GL_RENDERBUFFER_WIDTH, &wi);
glGetRenderbufferParameteriv(GL_RENDERBUFFER, GL_RENDERBUFFER_HEIGHT, &he);

glGenRenderbuffers(1, &depthBuf);
glBindRenderbuffer(GL_RENDERBUFFER, depthBuf);
glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT16, wi, he);

//还要记得开启深度测试
  glEnable(GL_DEPTH_TEST);

模型矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

glm::vec3 cubePositions[] = {
      glm::vec3( 0.0f,  0.0f,  0.0f),
      glm::vec3( 2.0f,  5.0f, -15.0f),
      glm::vec3(-1.5f, -2.2f, -2.5f),
      glm::vec3(-3.8f, -2.0f, -12.3f),
      glm::vec3( 2.4f, -0.4f, -3.5f),
      glm::vec3(-1.7f,  3.0f, -7.5f),
      glm::vec3( 1.3f, -2.0f, -2.5f),
      glm::vec3( 1.5f,  2.0f, -2.5f),
      glm::vec3( 1.5f,  0.2f, -1.5f),
      glm::vec3(-1.3f,  1.0f, -1.5f)
  };
  for(unsigned int i = 0; i < 10; i++)
  {
      //模型矩阵
      glm::mat4 model;
      model = glm::translate(model, cubePositions[i]);
      float angle = 20.0f * i;
      model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
      glUniformMatrix4fv(glGetUniformLocation(program, "model"), 1, GL_FALSE, glm::value_ptr(model));

      glDrawArrays(GL_TRIANGLES, 0, 36);
  }

这里的模型矩阵 将物体 进行位移,旋转后 放在世界坐标系中合适的位置.

观察矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13

定义了 相机的初始位置 与 初始方向(这里讲方向保持为单位向量)
glm::vec3 cameraLo = glm::vec3(10.0f,0.0f,0.0f);
glm::vec3 cameraDir = glm::vec3(1.0f,0.0f,0.0f);

.........其他代码.........


glm::mat4 view;
view = glm::lookAt(cameraLo,cameraLo-cameraDir, glm::vec3(0.0, 1.0, 0.0));

//将镜头观察点 保持为 镜头方向位置  向上方向 设置为y轴.

glUniformMatrix4fv(glGetUniformLocation(program, "view"), 1, GL_FALSE, glm::value_ptr(view));

在Display计时器中持续调用该方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

-(void)move{
    if (_isAdvance) {
        // 使摄像机 向朝向方向移动~~
        cameraLo -=(cameraDir*(speed/24));
    }
    if (_isback) {
        cameraLo +=(cameraDir*(speed/24));
    }
    
    //改变摄像机朝向
    if (_isLeft) {
        cameraDir = glm::normalize(glm::vec3(cameraDir[0],cameraDir[1],cameraDir[2]-rotateSpeed));
    }
    if (_isRight) {
        cameraDir = glm::normalize(glm::vec3(cameraDir[0],cameraDir[1],cameraDir[2]+rotateSpeed));
    }
    if (_isUp) {
        cameraDir = glm::normalize(glm::vec3(cameraDir[0],cameraDir[1]-rotateSpeed,cameraDir[2]));
    }
    if (_isDown) {
        cameraDir = glm::normalize(glm::vec3(cameraDir[0],cameraDir[1]+rotateSpeed,cameraDir[2]));
    }
    [self render];
}

demo地址

最终实现效果: